Геометрия. 7 класс. Глава II. Параграф 2. Тест 1. Вариант 1.
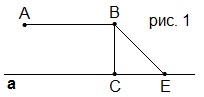 1. Какой из отрезков, изображённых на рисунке 1, является перпендикуляром к прямой а?
1. Какой из отрезков, изображённых на рисунке 1, является перпендикуляром к прямой а?
A) АВ; B) ВС; C) ВЕ; D) СЕ.
2. а) Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется … .
б) Сколько всего высот в треугольнике?
A) а) медианой; б) 3; B) а) высотой; б) 3;
C) а) биссектрисой; б) 2; D) а) медианой; б) 2.
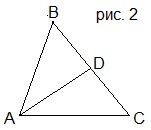 3. В треугольнике АВС (рис. 2) AD – биссектриса. ∠ВАС=70°, ∠АВС=60°. Найти ∠CAD.
3. В треугольнике АВС (рис. 2) AD – биссектриса. ∠ВАС=70°, ∠АВС=60°. Найти ∠CAD.
A) 30°; B) 40°;
C) 35°; D) 140°.
4. а) Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется … .
б) Сколько биссектрис можно провести в треугольнике?
A) а) биссектрисой; б) 3; B) а) медианой; б) 2;
C) а) высотой; б) 1; D) а) высотой; б) 3.
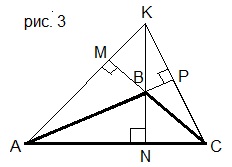 5. а) Назвать высоты треугольника АВС (рис. 3).
5. а) Назвать высоты треугольника АВС (рис. 3).
б) Назвать высоту треугольника АВС, проведённую из вершины А.
в) Назвать высоту треугольника АВС, проведённую к прямой, содержащей сторону АВ.
A) а) АМ, BP, CP; б) AN; в) CN; B) а) АP, BN, CM; б) AP; в) CB;
C) а) АМ, BA, CN; б) AM; в) CM; D) а) АМ, BN, CP; б) AM; в) CP.
6. Точки М и N лежат по одну сторону от прямой а. Перпендикуляры MK и NP к прямой а равны между собой. Найдите ∠MKN, если ∠NKP=43°36’.
A) 46°34’; B) 46°24’; C) 47°24’; D) 56°64’.
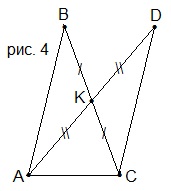 7. Найти ∠АСD (рис. 4), если ∠АСК=70°, ∠АВС=35°, ∠АDС=28°.
7. Найти ∠АСD (рис. 4), если ∠АСК=70°, ∠АВС=35°, ∠АDС=28°.
A) 63°; B) 35°; C) 105°; D) 45°.
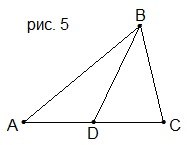 8. В треугольнике АВС (рис. 5) BD – медиана. АВ=12 см, АС=14 см. Периметр треугольника ABD равен 27 см. Найдите медиану BD.
8. В треугольнике АВС (рис. 5) BD – медиана. АВ=12 см, АС=14 см. Периметр треугольника ABD равен 27 см. Найдите медиану BD.
A) 8 см; B) 9 см; C) 10 см; D) 11 см.
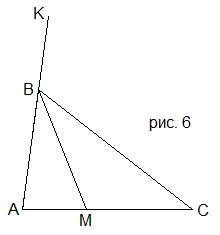 9. В треугольнике АВС (рис. 6) ВМ – биссектриса. ∠АВМ=32°. Найти ∠СВК.
9. В треугольнике АВС (рис. 6) ВМ – биссектриса. ∠АВМ=32°. Найти ∠СВК.
A) 148°; B) 116°; C) 64°; D) 126°.
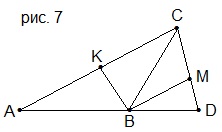 10. ВК – биссектриса треугольника АВС (рис. 7). ВМ – биссектриса треугольника ∠ВСD. Найти ∠КВМ.
10. ВК – биссектриса треугольника АВС (рис. 7). ВМ – биссектриса треугольника ∠ВСD. Найти ∠КВМ.
A) 45°; B) 60°; C) 100°; D) 90°.
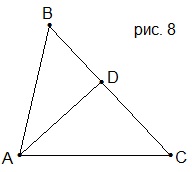 11. Биссектриса АD в треугольнике АВС (рис. 8) разделила сторону ВС, равную 20 см, в отношении 2 : 3, считая от вершины В. Найти BD и СD.
11. Биссектриса АD в треугольнике АВС (рис. 8) разделила сторону ВС, равную 20 см, в отношении 2 : 3, считая от вершины В. Найти BD и СD.
A) BD=6 см, СD=14 см; B) BD=5 см, СD=15 см;
C) BD=8 см, СD=12 см; D) BD=7 см, СD=13 см.
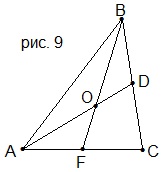 12. Каждая медиана треугольника точкой пересечения медиан делится в отношении 2 : 1, считая от вершины.
12. Каждая медиана треугольника точкой пересечения медиан делится в отношении 2 : 1, считая от вершины.
АD и BF — медианы (рис. 9). AD=12 см, BF=15 см. Найти AO и OF.
A) AO=8 см, OF=10 см; B) AO=8 см, OF=5 см;
C) AO=4 см, OF=5 см; D) AO=4 см, OF=10 см.
