Алгебра. 11 класс. Тест 0.
Вариант 1.
1. Представить бесконечную периодическую десятичную дробь 0,2(36) в виде несократимой обыкновенной дроби. В ответе записать сумму числителя и знаменателя.
1) 56; 2) 18; 3) 68; 4) 48.
2. Найти сумму бесконечно убывающей геометрической прогрессии:
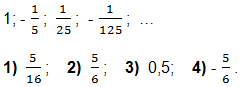
3. Вычислить:
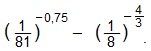
1) 21; 2) 12; 3) 16; 4) 11.
4. Найдите функцию, обратную к функции:

5. Решить иррациональное уравнение:
![]()
1) 3; 8; 2) -1; 7; 3) 1; 7; 4) 1.
6. Решить иррациональное неравенство:
![]()
1) -0,05; 1; 2) (-0,05; 1); 3) [-0,05; 1]; 4) (-∞; -0,05) U (1; +∞).
7. Решить показательное уравнение:
0,9 ∙ 3х = 2,7.
1) 2; 2) -1; 3) 0,5; 4) 1.
8. Вычислить: log3log2 8.
1) 4; 2) 3; 3) 2; 4) 1.
9. Решить логарифмическое уравнение: log4(3x-5) = 2.
1) 2; 2) 7; 3) 5; 4) 9.
10. Найти tgα, если угол α находится во второй четверти и sinα = 12/13.
1) -2,4; 2) 5/13; 3) -5/13; 4) 2,4.
11. Вычислить: 4 arccos 0 -3 arccos 1.
1) π; 2) -π; 3) 2π; 4) 3π.
12. Решить тригонометрическое уравнение:
![]()
1) π+2πk, k ϵ Z; 2) 2πk, k ϵ Z; 3) ±π/3+2πk, k ϵ Z; 4) πk, k ϵ Z.
Вариант 2.
1. Представить бесконечную периодическую десятичную дробь 0,32(4) в виде несократимой обыкновенной дроби. В ответе записать сумму числителя и знаменателя.
1) 298; 2) 152; 3) 168; 4) 248.
2. Найти сумму бесконечно убывающей геометрической прогрессии:

3. Вычислить:

1) 25; 2) 57; 3) 75; 4) 32.
4. Найдите функцию, обратную к функции:

5. Решить иррациональное уравнение:
![]()
1) 3; 5; 2) -1; 8; 3) -5; -3; 4) 5.
6. Решить иррациональное неравенство:
![]()
1) [-0,15; 1]; 2) -1; 0,15; 3) [-1; 0,15]; 4) (-∞; -1] U [0,15; +∞).
7. Решить показательное уравнение:
0,008 ∙ 5х = 0,04.
1) 2; 2) -1; 3) 1; 4) 0.
8. Вычислить: log2log3 81.
1) 4; 2) 3; 3) 2; 4) 1.
9. Решить логарифмическое уравнение: log7(4x+3) = 3.
1) 95; 2) 70; 3) 75; 4) 85.
10. Найти ctgα, если угол α находится в четвёртой четверти и cosα = 0,96.
1) -7/24; 2) 5/7; 3) 7/24; 4) -24/7.
11. Вычислить: 5 arcsin 1 + 3 arccos 0.
1) 5π; 2) 4π; 3) 3π; 4) 2π.
12. Решить тригонометрическое уравнение:
2sinxcosx=1
1) π/4+πk, k ϵ Z; 2) πk, k ϵ Z; 3) π/2+2πk, k ϵ Z; 4) π+πk, k ϵ Z.
